Oops on Starshot

You may remember the Starshot proposal: to use light sails and giant laser arrays to drive zillions of tiny space probes at nearby stars.

It turns out that the high acceleration phase might have some problems. High intensity lasers tend to shred photon sails. I gather the simulation shows that the mass of the electrons starts to become significant in the response of the conductive sheet. The article gives a pretty clear explanation, but the gist is that in order to reflect the light, the electrons in the conductor shuffle back and forth in response to the electric field of the light--but not perfectly. At high intensities the result is that the ions in the lattice of the metal get shaken too much.

So the light sail idea, while it may still work, will probably require lower intensities and a longer acceleration time. Pesky reality has a way of screwing up science fiction plans.

Sci-Fi

Is science fiction our era’s characteristic art form? Themes from it permeate the culture. I’ve overheard earnest conversations about how much they are looking forward to having their brains downloaded into a computer. And confident assertions that we’ll be able to cure criminal behavior. And that we’ll have FTL travel soon. Some of these were strangers, so I don’t think my observations are skewed by having odd friends. And SF (1960) described the equivalent of the Gaia Hypothesis before it got its name (circa 1973).

"What If" can be a wonderful question, and the setting for great stories. People will still read She years after the crop of novelists featured in today’s Entertainment section are forgotten dust. (They hit all the fashionable notes, and I’d rather watch paint dry. I think next decade's readers will agree.)

"What If," to yield a good story, has to have the rest of the environment stay familiar. If you have interstellar travel, and are writing about human beings, you will sooner or later have interstellar piracy and war. Familiar things. Too much "What If" and it gets hard to use the reader’s expectations. Think of what happened with the Marx brothers movies when they got full control--it was more chaotic and less funny.

A good "What If" can make you think, not just enjoy a good yarn. But if you immerse yourself in this, if "What If" is the sea your thoughts swim in, I’d suspect that your knowledge can wind up diluted in the flood of possibilities. We don’t always have a solid handle on things that aren’t part of our everyday work anyway.

The notion that we can define ourselves is clearly science fiction. When technology adds illusion to "What If" some people start to believe they can actually change sex. Or be unfrozen, resurrected, and cured. (As both Simak and Niven pointed out, why would future folks bother?)

The upside of "What If" is an optimism about problem solving—or at least that used to be the case with earlier sci-fi. I'm not able to say much about recent works. I gather quite a bit of the recent stuff is didactically PC, but that doesn’t get past my filters. Limited money and time... The downside of the upside is a belief that a few select wise people can solve problems for everybody, and ought to.

Perhaps these influences aren't overwhelming, but I seem to find small traces all over the place. Or I may be missing something, since I'm not plugged into pop culture very strongly.

Translations

A student from Spain joined our Thanksgiving crowd. She told us they had to study Don Quixote in school, and virtually nobody finished it. She asked if anybody else had. I pled guilty, and said I actually liked it--the sequel not so much. But I read it in translation, and she in archaic Spanish. Perhaps there was some poetry in the original that I completely missed, but the story by itself was fine enough to survive translation. I wonder if Shakespeare is easier in translation too.

Simple groups

This is a follow-on to my earlier post about sequences: alternative topics in math that a highschooler can pick up. (I tried this out on some 3'rd graders. I have no idea how much they remembered two weeks later.)

To begin, think about clocks.

This one is too complicated. Try something simple.

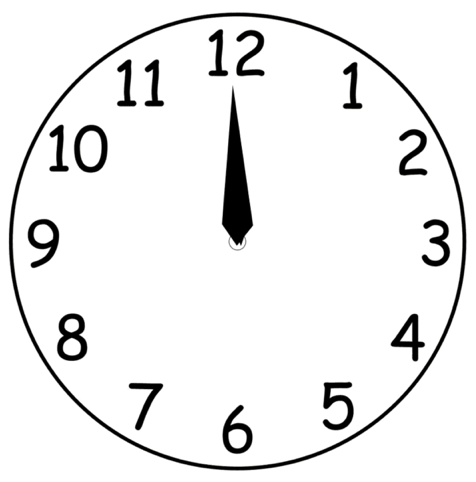
This one says 12 o’clock. Or just 12.

The left-hand clock above says 4. You can think of this several different ways. It could be the time of day: 4:00. Or it could mean 4 hours of time. Wait for 4 hours.

Let’s think of it the second way. You can add waits together. Waiting 4 hours, plus waiting 4 hours, is like waiting for 8 hours on the clock.

Suppose you start at some time (pick a time, any time, say 12:00) and wait for 4 hours, and then wait for 8 hours. What time is it?

As far as the clock is concerned, you’re right back where you were.

4 ⊕ 4=8, 4 ⊕ 8=12, and 8 ⊕ 8=4. In other words, clock counting wraps around itself. I use the symbol ⊕ instead of + because it isn’t quite like adding ordinary numbers.

We use the numbers 1-12, but you can just as easily use Roman numerals, or label the hours with degrees of rotation, or put Chinese numerals in place—whatever you please. The way this works doesn’t depend on the labels you give the elements. All “12-hour clocks” will behave the same way.

Notice a couple of things about the 12-hour clock.

1. Adding 12 to anything gives that same thing back again—just like adding zero. Rotating 360 degrees is just like not rotating at all.
2. Whatever you start with, you can always “add”something to get to 12. If you start with 3 you can “add” 9 to get to 12. If you rotate by 85 degrees, you can rotate by another 275 degrees to get back to where you started.

Those two qualities define what mathematicians call an “Identity” element. If you have one you can ⊕ it with anything and the other thing doesn’t change. And there’s always an “Inverse” to every other element in the set. Just like 1+ (-1) = 0, 5 ⊕ 7 = 12.

Something else that may seem pretty trivial here, but isn’t always true, is that so long as I keep the order the same I can combine terms any way I like. (1 ⊕ 2) ⊕ 4 = 1 ⊕ (2 ⊕ 4) = 7.

We have to specify this because in everyday life this isn’t always true. Take concentrated sodium hydroxide, concentrated sulfuric acid, and sugar. If I mix the first two first, and then add the sugar, nothing dramatic happens. If I add the sulfuric acid to the sugar first, the sugar chars. Adding sodium hydroxide afterwards doesn’t “unchar” the mix.

The 12-hour clock is an example of what are called “cyclic groups.” They obviously get the name because they go in cycles. You can have a 24-elements cycle, a million-element cycle, a 2-element cycles—and there’s only one of a given size. Different labels for the elements don’t matter, all 3-element cycles behave exactly the same, so there’s really only one kind.

Triangles

The order you do even two things in can matter. You don’t get the same result if you put on socks and then shoes as if you put on shoes and then socks. socks ⊕ shoes ≠ shoes ⊕ socks.

You may have seen the little trick with two dollar bills in which you give them the same rotations, but in different orders, and wind up with George facing one way on one and the opposite way on the other.

Try this with triangles. I numbered the vertices of the original triangle and the one we rotate and flip to make it easy to see what’s going on.

The object is to rotate or flip the triangle so that it fits back on its original spot. If you rotate by 90 degrees it won’t land right—you have to rotate by 120, 240, or 360 degrees. I call these rotations B, C, and A—but remember that the labels don’t matter. The three rotations together make a 3-cycle; a 3-element group.

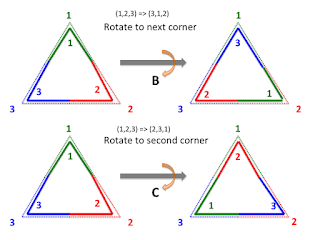
You can also flip the triangle, and there are 3 flips that bring it back to its original spot. If you flip it twice the same way, you get back to where you were before.

There aren’t any other rotations or flips that land it back where it was. Try it out for yourself, or count the number of ways the old vertices can match up with the new locations. There are only 6.

What do we get when we combine rotations and flips? I’ll save you the effort, but try it out yourself.

⊕	A	B	C	D	E	F
A	A	B	C	D	E	F
B	B	C	A	E	F	D
C	C	A	B	F	D	E
D	D	F	E	A	C	B
E	E	D	F	B	A	C
F	F	E	D	C	B	A

Flip D followed by Flip E looks like rotating the triangle by 120 degrees. Flip E followed by Flip D looks like rotating the triangle by 240 degrees. D ⊕ E ≠ E ⊕ D

This is a "group" which is not commutative. You may vaguely recall that word from math back in high school. It didn't matter in algebra or geometry--but it does matter here, in abstract algebra.

This group has 4 non-trivial subgroups: {A,B,C}, {A,D}, {A,E}, and {A,F}. There's more to say about this rather simple group, but the margin is too small to contain it.

Dogs

We were strolling through the meso-american section of the Milwaukee Public Museum, and I noticed that I didn't notice any figures of dogs. Was I not looking for the right features on the stylized images, or were they scarce to begin with? North American Indians had dogs--the South must have too.

Yes, of course. Chihuahuas, of course, among many others. And there were some paintings and some figures--the example Wikipedia links to looks very un-stylized and doggy. There was nothing about how frequently dogs were portrayed, but since they ate dogs they may not have thought them as quite as suitable for dramatic art as jaguars.

But one link leads to another(*)--did Indians domesticate coyotes? There aren't any Hare Indian's left, but maybe there are bones somewhere. The argument went that they looked like them (but other dogs do too), sounded like them (other dogs don't), other dogs hated them (as though they were another species). Not overwhelming arguments, but if people can find a little DNA somewhere, it might be worth checking. If wolves, and foxes, and culpeos, why not coyotes?

---

(*) Which leads to not getting any writing done...

UPDATE : See Retriever's detailed comment.

Antifragile

AVI recommended Antifragile, and I've started it. It does, as AVI says, demand an occasional time of cross-checking with your own experiences.

I know one example of how placidity hid information. When I lived in Liberia the place seemed quite stable. It had had wars in the past, but nothing significant lately, and the party line (one party) was that development was slowly happening and the future looked bright. I had no great interest in studying the political situation, and wasn't encouraged to, though Growth Without Development sat waiting on my parent's bookshelf. Not my business. And if some tribal Liberians weren't thrilled with the state of the state, they weren't likely to confide in a young American lad.

Tolbert made some changes, and was afraid to make others, and between growing expectations and some world-wide economic problems, there were problems. (I had headed off to college.) Then a coup(*) killed Tolbert, and Doe's rule was bad enough to provoke several counter-attacks, and finally a civil war with tribal splits. I didn't see any of this coming; it all looked quite peaceful. But a one-party state often looks peaceful.

I might have known better, with a little more observation and curiosity, but I was content in my bubble--like quite a few others up until just recently.

---

I notice that in his examples of "Interventionism" he includes "Copy editors trying to change your text," and says the iotrogenic cost is bland writing.

He's pretty down on "fragile" technology, so I wonder what he thinks of gas pipes. A small leak in a water pipe may or may not be a catastrophe (leaks in the floor above have been known to drip down to our server racks), but leaks in a gas pipe...

---

(*) Some conspiracies claim that the US was behind the coup. Given the kind of person Doe was, and his position at the time, this is inane.

Luther's take

"When, therefore, I learned, most illustrious prince, that your Lordship has been afflicted with a grave illness and that Christ has at the same time become ill in you, I counted it my duty to visit Your Lordship with a little writing of mine. I cannot pretend that I do not hear the voice of Christ crying out to me from Your Lordship's body and flesh and saying: "Behold I am sick." This is so because such evils as illness and the like, are not borne by us who are Christian, but by Christ himself, our Lord and Saviour, in whom we live"...

Gleaning the ungleaned

Years ago I read about jubilee and noticed that reversion didn't apply to city-dwellers (a short buy-back period, but no more). I looked at the land being farmed in back of our apartment complex and thought that if the whole complex grabbed a handful or three every day during harvest it would put a noticeable dent in the crop. In 5 days our complex could have probably snarfed up a quarter of the acre nearest us. A literal application of the principles wasn't going to work.

OK, cities are special cases, and industrial production doesn't fit the Leviticus paradigm very well. So how does one translate the principle of "not reaping to the edge of your field" into action in a modern environment?

One trivial thing I've done, or rather not done, is not pick up lost money. I used to, but after a while figured that a kid finding the dime would get more joy out it than I would, so I started letting it lie undisturbed, graduating to larger denominations over time. (I've never seen the original owner find it again, or even look for it.) There's no nobility in that--I can do without that dollar bill caught in the bushes without breathing hard (it isn't really even explicitly mine anyway)--I'm just trying to get a handle on the right attitude by being faithful in the least things. Least things first.

If you work in sales, you can cut the price a bit and take less commission if the client is poor. I don't know how many do that. Doctors and some lawyers sometimes do pro bono work. That's one equivalent of not gleaning to the edges. But if you're a janitor, or an IT manager, what's the equivalent? Giving money away is not the same thing at all. Widows and orphans and the disabled--yes, they often need direct support. But gleaning the ungleaned was work for the able-bodied without land or adequate employment of their own--they got food and self-respect and to be a model for their kids.

Another detail of the context is different: maintenance of a home is much harder. In most places around here you don't get to build without a plan for water and power and heat--and utility costs and taxes mean you need a non-trivial revenue stream just to stay in one place. That's not including repairs, which are an expense with houses anywhere. So either we should talk about a different paradigm for low cost housing (like the tiny house movement--but heating is a really big deal in winter!), or a "gleaning the ungleaned" that earns money.

I'd rather not reinvent the wheel here. Some folks are bound to have put some thought already into American equivalents of "gleaning the ungleaned," and some of that is probably useful. There'll be no silver bullet, of course--even the tiny houses have issues. (Imagine a little collection of them. Now imagine who will be staying in the neighborhood a year later.) I'm dubious of top down plans, unless the top dog happens to be God, and very few of the top dogs are.

Can anybody point me at who has done some reasonable work in this area, or thought through pros and cons?

Knowledge

From a link to a link, when I should have been doing more useful things... Daniel Ellsberg said that esoteric knowledge corrupts.

Not always--not if you can and want to share it that's another matter. But I see his point; tangentially seconded by a good authority that "knowledge puffs up."

Moat Around Murchison's Eye

Niven and Pournelle collaborated again, this time for a third Mote novel. If you haven't read the first, the description here won't matter. The Mote in God's Eye was good.

This one is competent, but a bit disappointing. A red herring is waved too hard, there's way more focus on love lives than is useful to the story, and several characters, though well-defined at first, become less distinguishable later on. Pournelle's been unwell: I wonder if he didn't push back enough.

It seemed a little odd that the Moties didn't try a very simple probe of the Crazy Eddie Point: a small craft with a big engine in the process of reversing direction just as it passes through. Time it correctly and it would come right back quickly enough to let the Moties get a record of what was on the other side.

It reads like a finale, though I suppose a sequel in another generation is possible.

"Stay Healthy this holiday"

An insert in the Wisconsin State Journal this morning had suggestions about how to work off the dinner: 30 minutes of football for a slice of pumpkin pie (370 calories), or 10 minutes of hiking for a dinner roll (90 calories). I've a counter-proposal: work off that pie with some low impact exercise in the form of a nice 4 hour nap. You'll need it after all the preparations.

Earthquake lights

I'd heard of them, but never seen any pictures. Now we even have movies.

No, I don't know what causes this. I guessed that it was electric discharge from large-scale piezoelectric effects as the rock cracks for miles and miles, but that's just a guess.

Look at it.

Radioactive Boy Scout RIP

Back in 2004 I wrote about The Radioactive Boy Scout: David Hahn, who tried to build a breeder reactor in his back yard--and got it to produce extra radiation. Not quite self-sustaining, but a noble effort. So to speak.

He died this September. The obit doesn't give any cause, but apparently as recently as 9 years ago he was trying to lay hands on radioactive material--americium from stolen smoke detectors. The obit didn't say whether he died of cancer.

He had his problems (pretty severe, if getting charged with theft for tiny quantities of americium is any indicator), but he dreamed big. A home-made reactor: that's deadly crazy. But cool.

Virtues gone wild

"The modern world is not evil; in some ways the modern world is far too good. It is full of wild and wasted virtues. When a religious scheme is shattered (as Christianity was shattered at the Reformation), it is not merely the vices that are let loose. The vices are, indeed, let loose, and they wander and do damage. But the virtues are let loose also; and the virtues wander more wildly, and the virtues do more terrible damage. The modern world is full of the old Christian virtues gone mad. The virtues have gone mad because they have been isolated from each other and are wandering alone. Thus some scientists care for truth; and their truth is pitiless. Thus some humanitarians only care for pity; and their pity (I am sorry to say) is often untruthful.

Orthodoxy, by G.K. Chesterton

It seems to describe the wild claims and counterclaims of the party faithful--full of righteous indignation because they, in fact, do have part of the truth.

Daylight Savings Time

I think the rabbit doesn't like it.

Does anybody have some numbers for how much energy/time/lives-lost-in-night-accidents we're supposed to save with this bi-annual jetlag?

A season for returns

The NYT says the networks are worried: they're all ready for the big election night,

But as television news gears up for 2016’s big finale, an intense public distrust in the media is threatening the networks’ traditional role as election night scorekeeper.

I watched election returns one night years ago. I have not been tempted to try the exercise again. From one quarter hour to the next the changes were small, and misleading without the "Well, this district usually votes Republican, and this one includes the cemetery and votes the other way" explanations.

It's not like watching a ball game, with dramatic offense and defense and obvious skill. It's pretty abstract, and slow, and unless you believe that your intense stare will help your side win, nothing you do matters anymore.

Part of problem is commentary. They don't say it in so many words, but "Why do you think the people of Kansas are so stupid?" or excitedly "Look, the good guys are winning!"

The next day will be good enough--or, in the case of the Presidential election, bad enough. I'm not going to be happy no matter who wins that one. (*)

Donald Sensing proposes to leave the radio and TV off, and watch a move that night. Good advice. I've a little project I should attend to...

(*) Looking at the polls, I strongly suspect that the machine will successfully get out the vote for Hillary. Looking at the lawn signs, I see 3:1 Hillary:Trump in hard left Dane county (!), and O(10:1) in the countryside. But I think that just reflects lack of enthusiasm; they'll vote for the party when the time comes.

A courtesy

Don't ask people how they voted. It is rude--why is a secret ballot any of your business? I don't think it's a good precedent to assume that that kind of information is available on demand.

On the flip side, I don't need to know who you voted for--or who you retroactively voted for now that you know the result. It's generally virtue signaling or prompting (I showed you mine, now you show me yours), though for ancient history it could be just background. Maybe you think you know what my motives are in picking one Senator over another. AVI would say that I probably only have a fuzzy picture of that myself, and that a lot of our reasoning is ex post facto rationalization.

I have, in the past, explained why I deprecated one candidate or another. (That's shooting fish in a barrel this election--and everybody else has done it already.) I doubt that I persuaded anybody, but I tried, and persuasion is part of the game. But still, don't ask. The man with the 6' Trump sign probably didn't vote for Jill Stein. Don't ask. (Do you floss every day? Don't ask. Boxers or briefs? Please don't ask.)

This year's presidential election I think shows even more clearly the value of this little courtesy.

Letting the punishment fit the crime

Police in Shenzhen (southern China) "are punishing drivers who dazzle other road users with full-beam headlights by making them stare into the lights for a minute".

"Shenzhen's traffic police have opted for unconventional penalties before. Last year, they made jaywalkers choose between paying a fine or wearing a green hat and vest while directing traffic."

Jubilation

My better half is a long-standing Cubs fan, who could probably have passed Royko's true fan quiz. "Lovable losers" has almost been the Cubs' trademark, but this year... Somebody pointed out that a number of the Cubs are Catholic, and Catholics have the Jubilee Year of Mercy this year.

Is my conclusion swayed by bias?

Protein is good for you, and the new results say that dietary fat is good for you. So I'm going to start classifying bratwurst as health food. Dress it with tomatoes (fruit), onions, pickles--you're getting close to a complete meal here. (The Lamaze instructor ages ago, when talking about morning sickness, said that pizza made a good meal.)