One of the bits describes the use of Feynman diagrams: Adding up all the various sub-processes that contribute to an overall interaction of some kind. A and B interact somehow to produce C and D, and all sorts of things can happen in the middle.
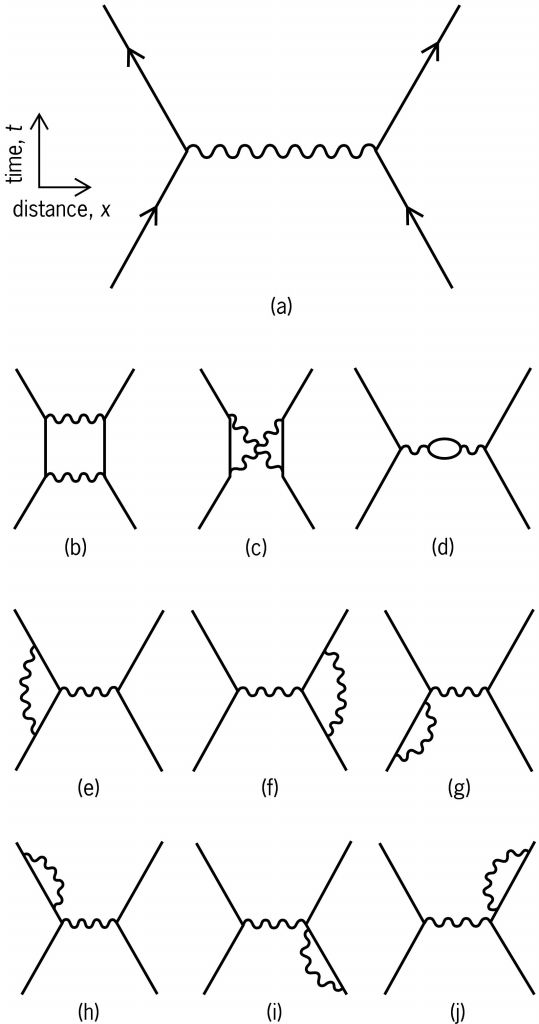
Yep, those are only a few. (See the video)
Each one of the diagrams represents a contribution that requires a messy integral to solve. With luck, the coupling at each connection is small, and the more and more complicated diagrams contribute less and less, so that you can reach "good enough" without too much pain. Without luck--and QCD doesn't have it--they can get bigger.
This formalism works beautifully for quantum electrodynamics.
The situation reminds me very strongly of epicycles. They work. "There is no bilaterally-symmetrical, nor eccentrically-periodic curve used in any branch of astrophysics or observational astronomy which could not be smoothly plotted as the resultant motion of a point turning within a constellation of epicycles, finite in number, revolving around a fixed deferent."
For Ptolemy's work he only needed to work with a few terms. But the epicycles don't show what's going on nearly as well as ellipses around the Sun. Of course the planetary interactions make our orbital calculations more complex than anything Ptolemy ever attempted, but to land probes we need way better precision than anything he ever attempted.
Lubos and O'Dowd think string theory is the tool we need to wrap up an infinite series of diagrams into a simple form: epicycles turn into universal gravitation and ellipses. I hope so, but I'm not sanguine about progress, given the lack of it so far, and the way supersymmetry is bound up with it. Supersymmetry itself seems rather epicyclic too: it lets you cancel out some divergences when trying to sum terms in perturbation theory. There's that business of adding up lots of finer and finer terms again.
No comments:
Post a Comment